Forschung

Das Mathematische Institut blickt auf eine über 125-jährige verpflichtende Tradition mathematischer Forschung zurück. Hervorgegangen ist es aus dem von Felix Klein im Jahr 1881 gegründeten Mathematischen Seminar.

Algebra

zur Vergrößerungsansicht des Bildes: Diagonalfläche von Clebsch
Diagonalfläche von Clebsch

Die Abteilung Algebra wird durch drei Professuren vertreten.

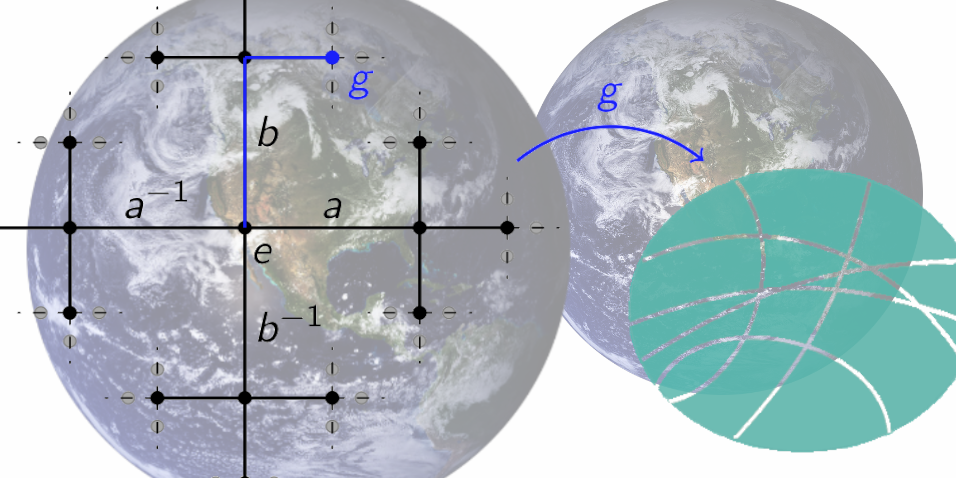
  • Professur für Algebra (Tobias Finis) mit Forschungsschwerpunkt in der Zahlentheorie: insbesondere automorphe Formen und Spektraltheorie mit Anknüpfungspunkten innerhalb des Instituts, zum Beispiel bei der Dynamik von Gruppenwirkungen 
  • Professur für Angewandte Algebra (Rainer Sinn) mit Forschungsschwerpunkt in der reellen algebraischen Geometrie:  insbesondere Spektraeder und klassische projektive Geometrie mit Bezügen zur diskreten Geometrie und Optimierung, Computer Vision und theoretischen Informatik
  • Professur für Theoretische Mathematik (Łukasz Grabowski)

In der Abteilung Algebra bestehen enge Kooperationen mit nationalen und internationalen Forschungsinstituten, unter anderem mit dem Max-Planck Institut für Mathematik in den Naturwissenschaften oder dem Weizmann-Institut (Israel).

 

Analysis

zur Vergrößerungsansicht des Bildes: Symbolbild Analysis
Symbolbild Analysis / Jonas Hirsch/Mathematisches Institut, Uni Leipzig

Die Analysis bildet einen der traditionellen Schwerpunkte der Leipziger Mathematik. Dies zeichnet sich einerseits durch die starke personelle Ausstattung der Abteilung, andererseits durch die enge inhaltliche und personelle Verzahnung mit dem Max-Planck-Institut für Mathematik in den Naturwissenschaften aus. In der Forschung positioniert sich die Abteilung international an vorderster Stelle im Bereich der modernen Theorie partieller Differentialgleichungen, mit einer stark anwendungsorientierten Ausprägung besonders in der Kontinuums- und Hydrodynamik, Variationsrechnung, mathematischen Physik und Geometrie - eine Leipziger Besonderheit. Durch diese Fokussierung werden zahlreiche inhaltliche Verbindungen zu anderen Fachbereichen gestärkt, beispielsweise mit der Wahrscheinlichkeitstheorie und Ergodentheorie sowie der theoretischen Physik.

 

Didaktik der Mathematik

zur Vergrößerungsansicht des Bildes: Symbolbild Didaktik der Mathematik
Symbolbild Didaktik der Mathematik / Thomas Krohn/Mathematisches Institut, Uni Leipzig

Die Abteilung Didaktik der Mathematik erforscht das Lehren und Lernen von Mathematik, insbesondere in der Sekundarstufe. Untersuchungsgegenstand sind hier unter anderem Schülervorstellungen und ihr Einfluss auf den Lernprozess. Dabei wird die ganze Spannbreite von der Diagnose und Therapie von Dyskalkulie in der Sekundarstufe 1 bis hin zum Übergang Schule-Hochschule erforscht. Ein methodischer Schwerpunkt liegt auf der Einbindung von Lehr-Lern-Laboren sowie dem Einsatz von Mathematikgeschichte im Schulunterricht. Letzteres ist das Bindeglied zum zweiten Themenschwerpunkt der Abteilung, der Geschichte der Mathematik im 16. und 17. Jahrhundert sowie der mathematischen Modelle des 19. Jahrhunderts, in dem auch die Modellsammlung von Felix Klein betreut wird.

Die Abteilung kooperiert eng mit den mitteldeutschen Fachdidaktiken und engagiert sich im Arbeitskreis Lehr-Lern-Labore in der GDM. Darüber hinaus bestehen mehrere internationale und interdisziplinäre Kooperationen, beispielsweise mit dem Institut für Psychologie der Universität Graz in der Erforschung von Schülervorstellungen. Eine gemeinsame Graduiertengruppe mit Akteuren aus anderen Fakultäten der Universität Leipzig befindet sich im Aufbau.
 

 

 

Funktionalanalysis

zur Vergrößerungsansicht des Bildes: Symbolbild Funktionalanalysis
Symbolbild Funktionalanalysis / Felix Pogorzelski/Mathematisches Institut, Uni Leipzig

Die Abteilung Funktionalanalysis an unserem Institut wird vertreten durch die Professur für Funktionalanalysisvon Tatjana Eisner (z.Zt. vertreten durch Marcel Schmidt), sowie durch die Felix-Klein-Juniorprofessur von Felix Pogorzelski. Ausgehend von klassischen Grundlagen bietet die moderne Forschung im funktionalanalytischen Bereich mannigfaltige Möglichkeiten zur Spezialisierung.

Unsere zentralen Schwerpunkte sind Operator- und Spektraltheorie, sowie die Theorie dynamischer Systeme. Besonders spannend sind Problemstellungen im Schnittfeld dieser Bereiche. Entsprechende Lösungen finden zahlreiche mathematische Anwendungen, z.B. in der Zahlentheorie oder in der mathematischen Physik. Dabei ergeben sich natürliche Verbindungen zu den anderen Abteilungen unseres Instituts, darunter Analysis (via Spektraltheorie und Analysis), Geometrie und Algebra (via Dynamik von Gruppen), sowie Wahrscheinlichkeitstheorie (via Rekurrenzphänomene).

Geometrie

zur Vergrößerungsansicht des Bildes: Symbolgrafik Geometrie
Phasendiagramm eines Hamiltonschen Systems (M. Schwarz) — Komplexe Geometrie (J. Brinkschulte)

Die Abteilung Geometrie ist durch drei Professuren (Brinkschulte, Rademacher, Schwarz) vertreten.

  • Die Symplektische Geometrie (Prof. Schwarz) stellt die strukturmathematischen Beschreibungen der Räume für Hamiltonsche Dynamische Systeme zur Verfügung, welche selbst als wichtige Thematik der Mathematischen Physik vielfältige Bezüge zu weiteren naturwissenschaftlichen Gebieten aufweisen. Der Fokus der mathematischen Forschung liegt auf den Starrheitsphänomenen dieser Systeme und der zugrundeliegenden Geometrie. Dazu gehört insbesondere die Floer-Theorie (Arnold-Vermutung, Lagrange-Schnitte), die Methode der J-holomorphen Kurven und die Quantenkohomologie.

  • In der Riemannschen Geometrie (Prof. Rademacher) wird der Zusammenhang zwischen Krümmung, spektralen Eigenschaften von Differentialoperatoren und topologischen Invarianten untersucht. Ausserdem werden mit Hilfe der äquivarianten Morse-Theorie auf dem freien Schleifenraum unter geeigneten topologischen Annahmen Existenzresultate für periodische geodätische Linien hergeleitet.

  • In der Komplexen Geometrie (Prof. Brinkschulte) werden Mannigfaltigkeiten mit zusätzlichen Strukturen untersucht, u.a. komplexe, Kähler und CR Strukturen sowie Blätterungen. Analytische Methoden, insbesondere L²-Theorie für Cauchy-Riemann-Operatoren, spielen bei den Untersuchungen eine entscheidende Rolle. Neben Einbettungsproblemen stehen besonders Fragestellungen an der Schnittstelle zur komplexen Dynamik im Fokus, wie z.B. Klassifikation von Levi-flachen CR Mannigfaltigkeiten und dynamische Aspekte holomorpher Blätterungen.

Numerische Mathematik

zur Vergrößerungsansicht des Bildes: Numerische Simulation
Numerische Simulation / Mira Schedensack, Mathematisches Institut, Uni Leipzig

Die Numerik ist mit zwei Professuren vertreten.

  • Die Professur Numerik und Wissenschaftliches Rechnen (Peter Kunkel) befasst sich mit der numerischen Behandlung von Randwertproblemen, sowie mit der analytischen und numerischen Behandlung von differentiell-algebraischen Gleichungen. Weitere Forschungsschwerpunkte sind die Numerische Pfadverfolgung und Erweiterte Systeme zur Berechnung von singulären Punkten.
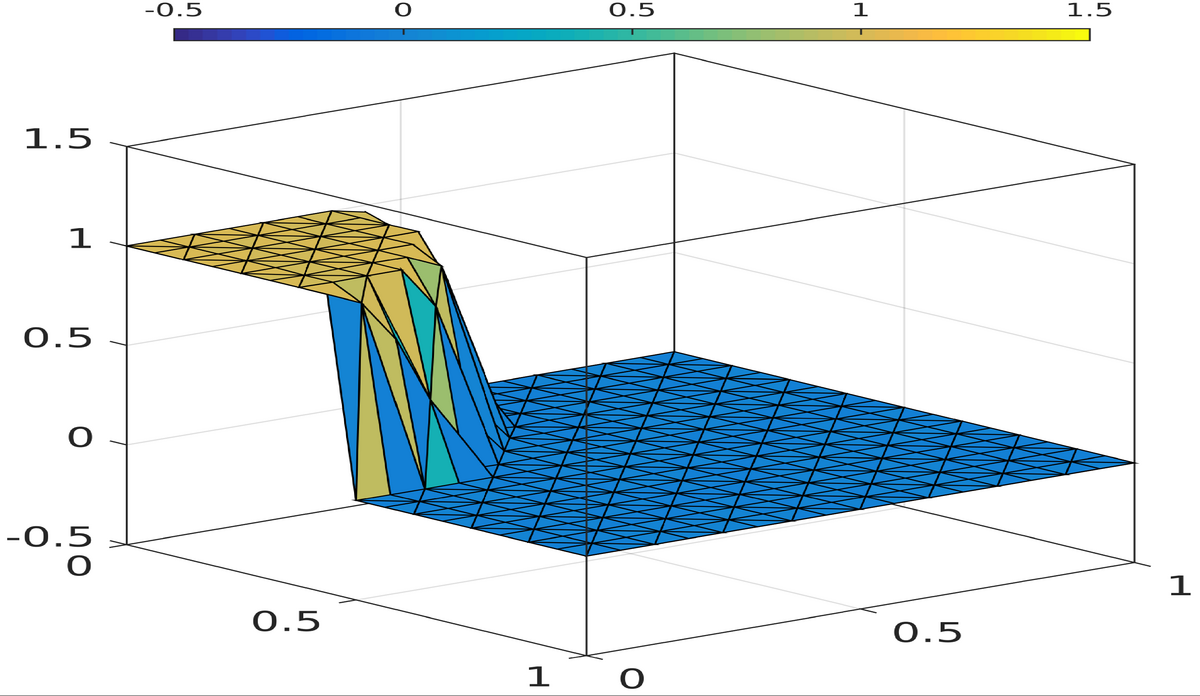
  • Die Forschung der Juniorprofessur für Numerik (Mira Schedensack) umfasst die Numerik für partielle Differentialgleichungen, insbesondere deren systematischer Fehleranalyse bei der Auflösung von Singularitäten und Mikrostrukturen. Hierbei werden zum Beispiel adaptive Finite-Elemente-Methoden für partielle Differentialgleichungen aus der Mechanik oder auch für Differentialgleichungen höherer Ordnung entwickelt.

Daraus resultieren Anknüpfungen zur Analysis, insbesondere durch die Nutzung strukturerhaltender Methoden in der Hydrodynamik, und Verbindungen zum MPI bei numerischer Homogenisierung und der Anwendung von Mehrskalenmethoden.

 

 

Stochastik

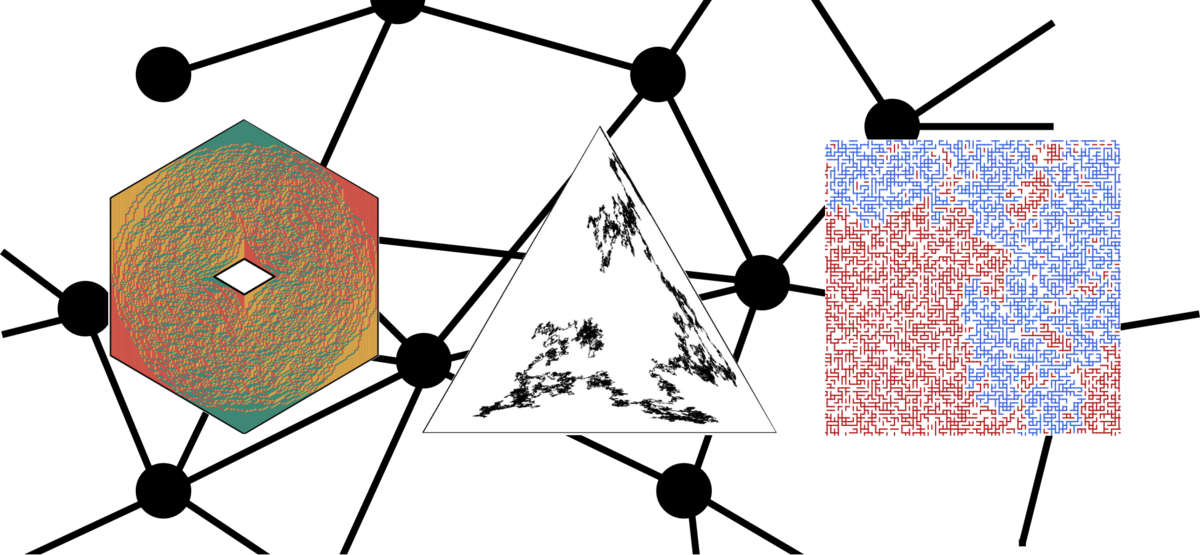
zur Vergrößerungsansicht des Bildes: Symbolbild Stochastik
(l) Random lozenge tiling (sim. by A. Bufetov), (c) Brownian motion on a simplex (sim. by T. Lehmann), (r) critical Bernoulli percolation / Artem Sapozhnikov, Mathematisches Institut, Uni Leipzig

Stochastik befasst sich mit der mathematischen Modellierung und Analyse zufälliger Phänomene. Am mathematischen Institut wird Stochastik durch drei Professuren und eine Juniorprofessur vertreten. Die Gruppe beschäftigt sich mit verschiedenen aktuellen Themen, die durch mathematische Physik und Biologie motiviert sind, insbesondere stochastische partielle Differentialgleichungen, integrable Gittermodelle, interagierende Teilchensystemen, Perkolation, stochastische Populationsmodelle und Zufallsgraphen.

Es bestehen enge Kooperationen mit dem Max-Planck-Institut für Mathematik in der Naturwissenschaften. Die Stochastikgruppe beteiligt sich an dem gemeinsamen Analysis-Probability-Seminar und am IMPRS-Graduiertenkolleg.

 

Das könnte Sie auch interessieren

Unser Forschungs­profil­bereich

mehr erfahren

Promotionen

mehr erfahren

Habilitationen

mehr erfahren